Investigating large datasets in R
Overview
Teaching: min
Exercises: minQuestions
How can we evaluate direct relationships between two variables?
How can we evaluate more complex relationships between multiple, interacting variables?
Objectives
Explore a large dataset graphically
Develop simple models with
lm()Choose new packages and interpret package descriptions
Analyze complex models using Information Theoretic (IT) Model Averaging (
armandMuMInpackages)
Setup
Let’s begin by loading the data and packages necessary to start this lesson.
# Load packages
library(ggplot2)
# Load data
phys_data<-read.csv("data/Physiology_Environmental_Data.csv")
Exploring the dataset
In previous lessons we’ve worked with the plant physiology dataset from O’Keefe and Nippert 2018. As a reminder, these data were collected to address the following objectives:
- How do nocturnal and daytime transpiration vary among coexisting grasses, forbs, and shrubs in a tallgrass prairie?
- What environmental variables drive nocturnal transpiration and do these differ from the drivers of daytime transpiration?
- Are nocturnal transpiration and stomatal conductance associated with daytime physiological processes?
We’ll use this dataset to explore the relationships between leaf transpiration and potential drivers of transpiration
Transpiration parameters:
- Nocturnal transpiration (Trmmol_night)
- Nocturnal stomatal conductance (Cond_night)
- Daytime transpiration (Trmmol_day)
- Daytime stomatal conductance (Cond_night)
Potential drivers:
- Nocturnal vapor pressure deficit (VPD_N)
- Nocturnal air temperature (TAIR_N)
- Daytime vapor pressure deficit (VPD_D)
- Daytime air temperature (TAIR_D)
- Daily average soil moisture (Soil_moisture)
- Predawn leaf water potential (PD)
- Midday leaf water potential (MD)
- Photosynthesis (Photo)
- Plant functional group (Fgroup)
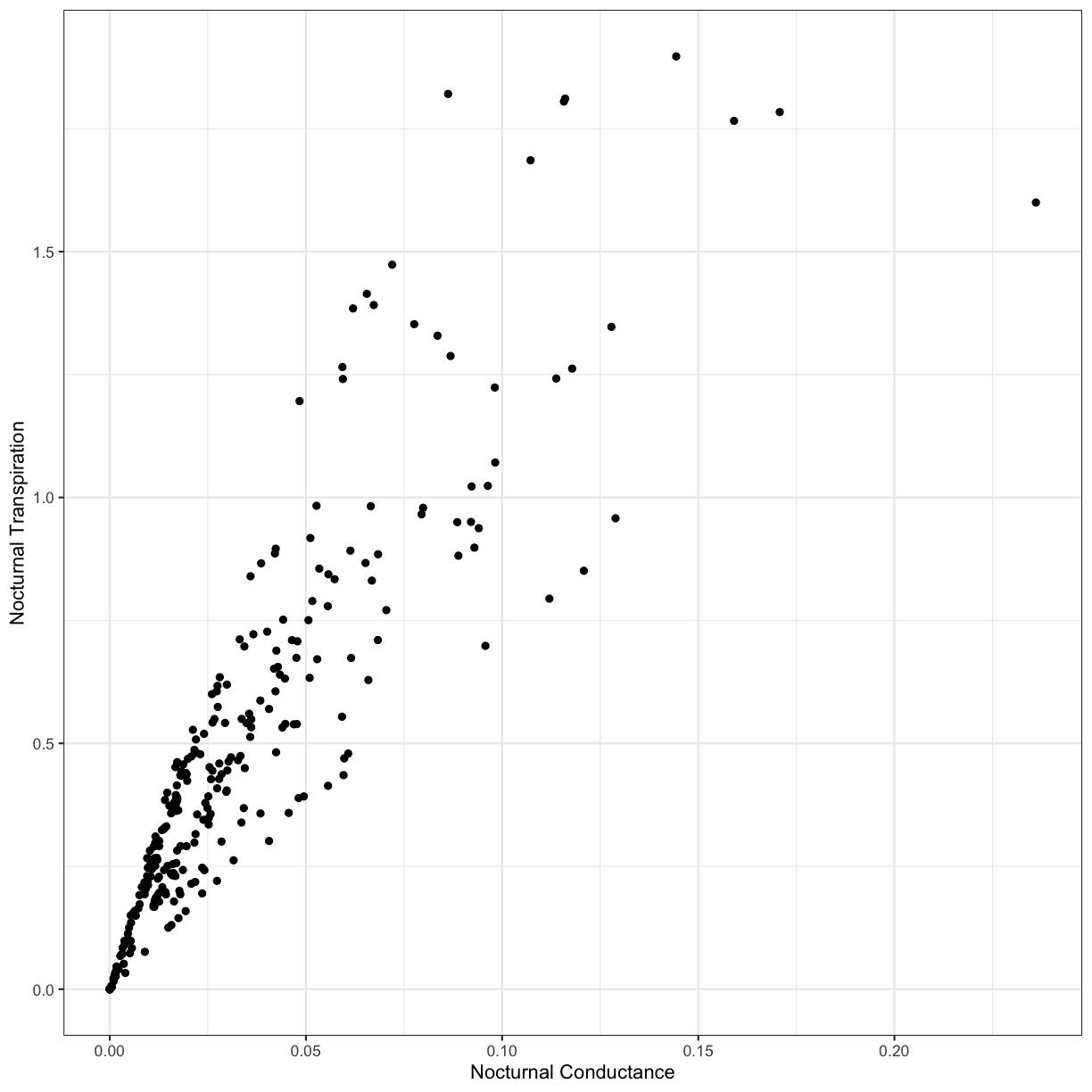
First, let’s review plotting in ggplot and investigate the relationship between nocturnal transpiration and nocturnal stomatal conductance.
Challenge 1
Use ggplot to create a scatterplot of the relationship between nocturnal transpiration and nocturnal stomatal conductance.
Solution to Challenge 1
# Nocturnal transpiration vs. nocturnal stomatal conductance ggplot(phys_data, aes(x=Cond_night, y=Trmmol_night)) + geom_point() + xlab("Nocturnal Conductance") + ylab("Nocturnal Transpiration") + theme_bw()
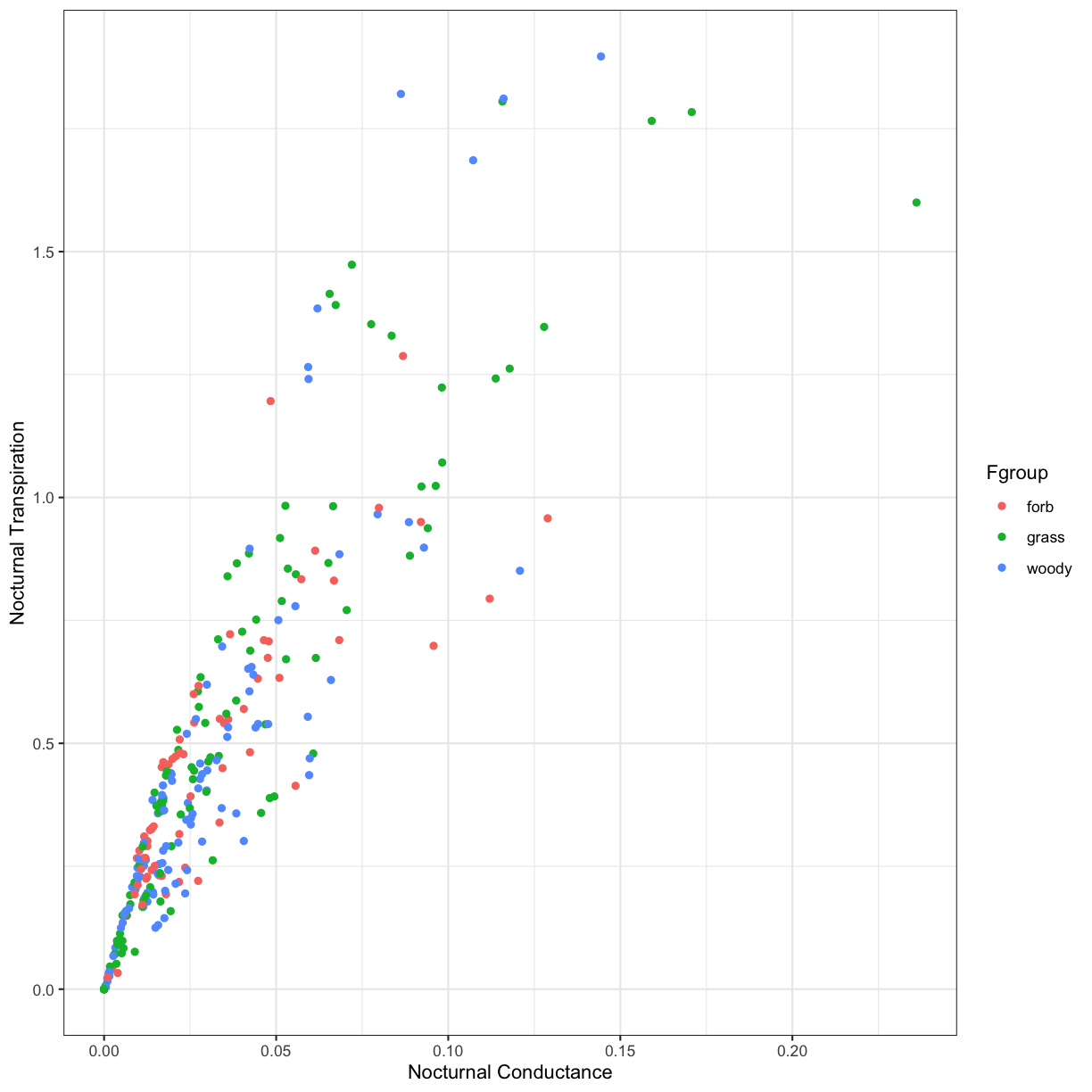
Challenge 2
Does this relationship differ between the different plant functional groups (grass, forb, woody)?
Solution to Challenge 2
ggplot(phys_data, aes(x=Cond_night, y=Trmmol_night, color=Fgroup)) + geom_point() + xlab("Nocturnal Conductance") + ylab("Nocturnal Transpiration") + theme_bw()
Using a Simple Model
As you can see, plotting our data can be informative, but it doesn’t necessarily tell us much about the statistical relationships between variables. We are going to start investigate the relationships between these data by using a simple linear regression. Linear regression is used to predict the value of a dependent variable Y based on one or more input independent (predictor) variables X, with the following basic equation:
In this equation, is the dependent variable, is the intercept, is the slope, and is the error term.
To build this equation in R, we’ll use the lm() function. lm() is included in the base R package, so you don’t have to load it into your workspace to use. lm() takes three basic arguments: the dependent variable, the independent variable, and the dataframe from which the data is used. The model is specified using a particular format, and is typically assigned to an object:
model_name <- lm(dependent_variable ~ independent_variable, data=dataframe_name )
We can then view our model output with the summary() function.
fit_trmmol <- lm(Trmmol_night ~ Cond_night, data=phys_data)
summary(fit_trmmol)
Call:
lm(formula = Trmmol_night ~ Cond_night, data = phys_data)
Residuals:
Min 1Q Median 3Q Max
-0.98937 -0.09752 -0.01945 0.07498 0.78951
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.13433 0.01548 8.68 3.31e-16 ***
Cond_night 10.39960 0.33128 31.39 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1843 on 280 degrees of freedom
Multiple R-squared: 0.7787, Adjusted R-squared: 0.778
F-statistic: 985.5 on 1 and 280 DF, p-value: < 2.2e-16
From this output, we’re usually interested in the following results:
-
(Intercept) Estimate: This is the y-intercept of our regression -
VPD_N Estimate: This is the slope of our regression -
Std. Error: The standard error for our intercept and slope estimates -
Pr(>|t|): These are the p-values associated with the intercept and our independent variable -
Multiple R-squared: The value that indicates model fit -
F-statisticandp-value: Indicate overall model significance
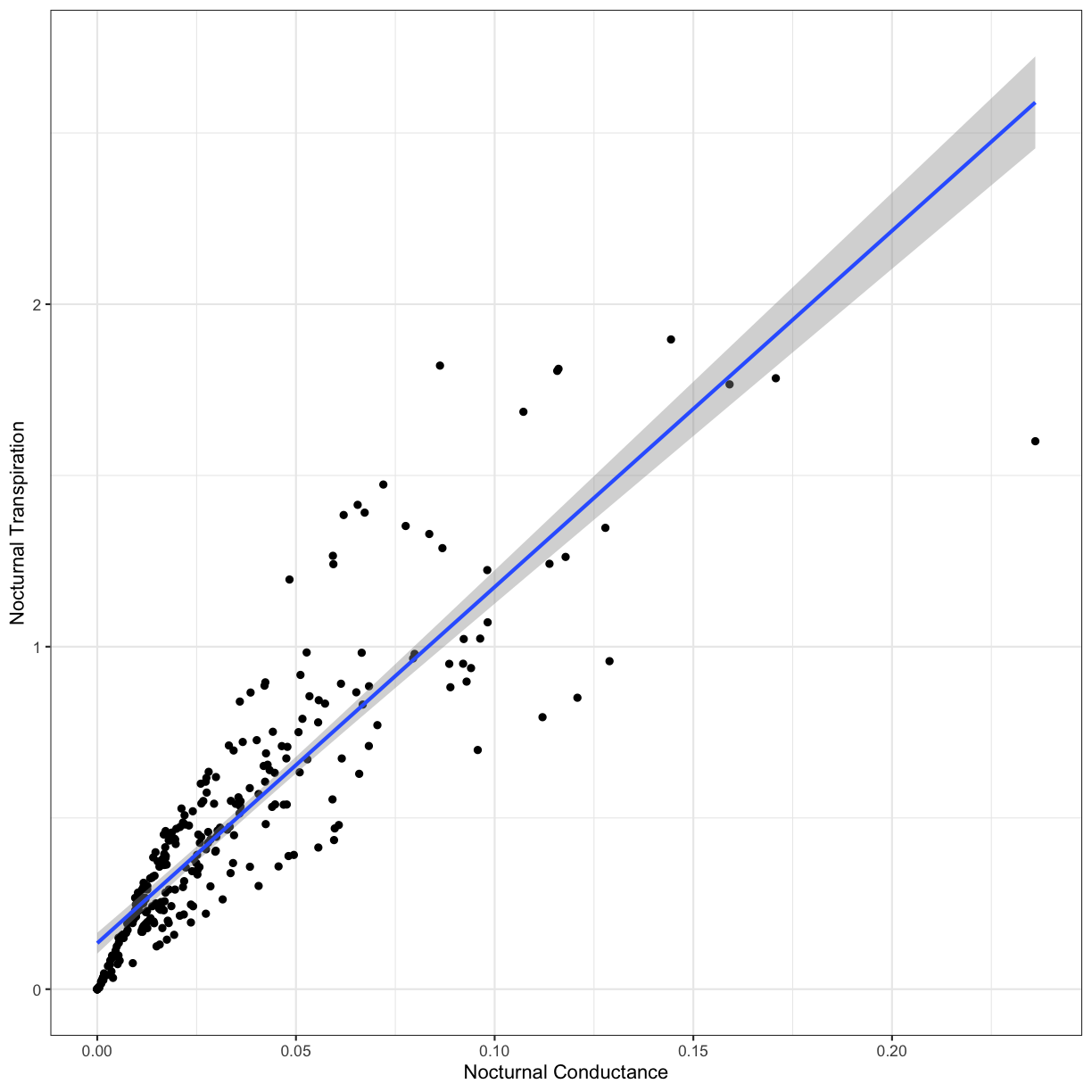
As you can see, there is a significant positive relationship between nocturnal transpiration and nocturnal conductance. This makes sense; as plant stomata open, more water can escape from the leaf. Let’s visual this regression on our scatterplot with geom_smooth():
ggplot(phys_data, aes(x=Cond_night, y=Trmmol_night)) +
geom_point() +
geom_smooth(method='lm') +
xlab("Nocturnal Conductance") +
ylab("Nocturnal Transpiration") +
theme_bw()
More Complex Models
Now that we know how to test for the effect of one variable on the dependent variable, let’s test for the effect of multiple variables on the dependent variable. This will be especially useful for understanding what drives nocturnal transpiration and nocturnal conductance, as there are likely multiple, interacting drivers for these parameters.
You can add additional variables to your model by using the following formula:
model_name <- lm(dependent_variable ~ independent_variable_1 * independent_variable_2, data=dataframe_name )
Note that adding an asterisk * between the two independent variables indicates that we will be testing for the effects of independent variable 1, independent variable 2, and their interaction on the dependent variable. If we were not interested in testing for interactions among independent variables, we could replace the * with a + sign.
Challenge 3
Create a model that tests for the effects of four factors on either transpiration or stomatal conductance.
Solution to Challenge 3
fit_all <- lm(Trmmol_night ~ VPD_N * TAIR_N * Soil_moisture * Fgroup, data=phys_data) summary(fit_all)Call: lm(formula = Trmmol_night ~ VPD_N * TAIR_N * Soil_moisture * Fgroup, data = phys_data) Residuals: Min 1Q Median 3Q Max -0.79840 -0.20271 -0.05773 0.12702 1.42836 Coefficients: Estimate Std. Error t value (Intercept) -4.224992 3.607216 -1.171 VPD_N 2.809890 6.789476 0.414 TAIR_N 0.269662 0.188632 1.430 Soil_moisture 24.056256 23.860637 1.008 Fgroupgrass -2.300135 4.622194 -0.498 Fgroupwoody 2.784390 4.582030 0.608 VPD_N:TAIR_N -0.177891 0.287298 -0.619 VPD_N:Soil_moisture -7.433865 52.156806 -0.143 TAIR_N:Soil_moisture -1.408985 1.231951 -1.144 VPD_N:Fgroupgrass 6.761417 8.445400 0.801 VPD_N:Fgroupwoody 0.766499 8.434074 0.091 TAIR_N:Fgroupgrass 0.134513 0.243379 0.553 TAIR_N:Fgroupwoody -0.172222 0.240418 -0.716 Soil_moisture:Fgroupgrass 28.520689 30.394684 0.938 Soil_moisture:Fgroupwoody -13.406242 30.119156 -0.445 VPD_N:TAIR_N:Soil_moisture 0.661956 2.176396 0.304 VPD_N:TAIR_N:Fgroupgrass -0.318487 0.359046 -0.887 VPD_N:TAIR_N:Fgroupwoody 0.008865 0.357972 0.025 VPD_N:Soil_moisture:Fgroupgrass -75.146534 64.206261 -1.170 VPD_N:Soil_moisture:Fgroupwoody -16.251816 64.126051 -0.253 TAIR_N:Soil_moisture:Fgroupgrass -1.426020 1.582136 -0.901 TAIR_N:Soil_moisture:Fgroupwoody 0.882050 1.561290 0.565 VPD_N:TAIR_N:Soil_moisture:Fgroupgrass 3.315745 2.691432 1.232 VPD_N:TAIR_N:Soil_moisture:Fgroupwoody 0.417599 2.684198 0.156 Pr(>|t|) (Intercept) 0.243 VPD_N 0.679 TAIR_N 0.154 Soil_moisture 0.314 Fgroupgrass 0.619 Fgroupwoody 0.544 VPD_N:TAIR_N 0.536 VPD_N:Soil_moisture 0.887 TAIR_N:Soil_moisture 0.254 VPD_N:Fgroupgrass 0.424 VPD_N:Fgroupwoody 0.928 TAIR_N:Fgroupgrass 0.581 TAIR_N:Fgroupwoody 0.474 Soil_moisture:Fgroupgrass 0.349 Soil_moisture:Fgroupwoody 0.657 VPD_N:TAIR_N:Soil_moisture 0.761 VPD_N:TAIR_N:Fgroupgrass 0.376 VPD_N:TAIR_N:Fgroupwoody 0.980 VPD_N:Soil_moisture:Fgroupgrass 0.243 VPD_N:Soil_moisture:Fgroupwoody 0.800 TAIR_N:Soil_moisture:Fgroupgrass 0.368 TAIR_N:Soil_moisture:Fgroupwoody 0.573 VPD_N:TAIR_N:Soil_moisture:Fgroupgrass 0.219 VPD_N:TAIR_N:Soil_moisture:Fgroupwoody 0.876 Residual standard error: 0.3611 on 258 degrees of freedom Multiple R-squared: 0.2172, Adjusted R-squared: 0.1474 F-statistic: 3.113 on 23 and 258 DF, p-value: 5.543e-06
How to Work with Complex Models: IT Model Averaging
As you can see, we have a lot of potential interactions with just four independent variables in our model! This becomes incredibly difficult to interpret, so we often have to look for other methods to analyze complex relationships in our data.
Although there are many different and valid ways to approach a statistical problem, today we are going to use Information Theoretic (IT) Model Averaging. Rather than creating a model with all possible variables and interactions, IT Model Averaging:
-
Compares mulitple competing models using information criteria
-
Ranks and weights each competing model
-
Averages a top model set to produce a final model that only includes predictor variables represented in the top model set
IT Model Averaging quantifies multiple competing hypotheses and is better able to avoid over-parameterization than traditional methods using a single model. To get started, we need to create a “global model” that includes all possible predictor variables. To simplify things even further, let’s only consider pairwise interactions among predictors. For this, R syntax supports polynomial expansions: you can write the terms as an additive model, then place the set of terms for which you want pairwise interactions in parentheses and square the sum, as in (x + y)^2.
model_name <- lm(dependent_variable ~ (independent_variable_1 + independent_variable_2)^2, data=dataframe_name )
# Global model
fit_IT <- lm(Trmmol_night ~ (VPD_N + TAIR_N + Soil_moisture + Fgroup)^2, data=phys_data)
IT Model Averaging requires the following packages:
arm: Includes thestandardize()function that standardizes the input variablesMuMIn: Thedredge()function creates a full submodel set, theget.models()function creates a top model set, andmodel.avg()creates the average model andimportance()calculates relative importance.
Let’s install and load these packages before we begin:
# Install packages
install.packages("arm")
install.packages("MuMIn")
# Load packages
library(arm)
library(MuMIn)
Before we start using these functions, let’s take a look at the package descriptions for arm and MuMIn
Note: When reading package descriptions, it is important to:
-
Read the overall package description. This will give you a good overall idea of what this package does, and if it would be useful for you.
-
Identify particular functions of interest. You don’t necessarily need to read the documentation for all of the functions within a package (typically, you’ll only use a few functions).
-
For individual functions, read through the basic description, usage, argument descriptions, details / notes, and examples. This will tell you what syntax to use and what the syntax means.
-
You can access package descriptions online (google search), from the CRAN website, or by using the
help()function in R.
First, let’s standardize our input variables with the standardize() function in the arm package. standardize() rescales numeric variables that take on more than two values to have a mean of 0 and a standard deviation of 0.5. To do this, we just need to specify the object to standardize (our global model, fit_IT):
# Standardize the global model
stdz.model<-standardize(fit_IT)
summary(stdz.model)
Call:
lm(formula = Trmmol_night ~ (z.VPD_N + z.TAIR_N + z.Soil_moisture +
Fgroup)^2, data = phys_data)
Residuals:
Min 1Q Median 3Q Max
-0.69948 -0.21909 -0.06959 0.13788 1.48475
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.50765 0.06199 8.189 1.1e-14 ***
z.VPD_N -0.29681 0.18108 -1.639 0.10237
z.TAIR_N 0.25517 0.18549 1.376 0.17007
z.Soil_moisture -0.07790 0.09859 -0.790 0.43015
Fgroupgrass 0.08123 0.05679 1.430 0.15381
Fgroupwoody -0.02886 0.05644 -0.511 0.60960
z.VPD_N:z.TAIR_N -0.12601 0.18162 -0.694 0.48841
z.VPD_N:z.Soil_moisture 0.49627 0.26345 1.884 0.06069 .
z.VPD_N:Fgroupgrass -0.01030 0.20095 -0.051 0.95915
z.VPD_N:Fgroupwoody 0.06443 0.20076 0.321 0.74853
z.TAIR_N:z.Soil_moisture -0.36228 0.23247 -1.558 0.12033
z.TAIR_N:Fgroupgrass -0.28903 0.20357 -1.420 0.15682
z.TAIR_N:Fgroupwoody -0.11230 0.20289 -0.554 0.58038
z.Soil_moisture:Fgroupgrass 0.36120 0.12340 2.927 0.00372 **
z.Soil_moisture:Fgroupwoody 0.20905 0.12133 1.723 0.08606 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.366 on 267 degrees of freedom
Multiple R-squared: 0.1677, Adjusted R-squared: 0.1241
F-statistic: 3.844 on 14 and 267 DF, p-value: 5.864e-06
Next, we create the full submodel set with the dredge() function in the MuMIn package by specifying the object that dredge() will evaluate (our standardized model, stdz.model). We also need to change the default “na.omit” to prevent models from being fitted to different datasets in case of missing values using options(na.action=na.fail) :
options(na.action=na.fail)
model.set<-dredge(stdz.model)
The get.models() function will then create a top model set. First, we need to specify the object that get.models will evaluate (our model set, model.set), and then we need to specify the subset of models to include all models within 4AICcs with subset=delta<4:
top.models<-get.models(model.set, subset=delta<4)
top.models
$`92`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.VPD_N +
Fgroup:z.Soil_moisture + Fgroup:z.VPD_N + 1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.45599 0.08474
Fgroupwoody z.Soil_moisture
-0.02706 -0.05451
z.VPD_N Fgroupgrass:z.Soil_moisture
-0.08277 0.30260
Fgroupwoody:z.Soil_moisture Fgroupgrass:z.VPD_N
0.18432 -0.24586
Fgroupwoody:z.VPD_N
-0.02848
$`64`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.TAIR_N +
z.VPD_N + Fgroup:z.Soil_moisture + Fgroup:z.TAIR_N + 1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.45588 0.08438
Fgroupwoody z.Soil_moisture
-0.02715 -0.08780
z.TAIR_N z.VPD_N
0.13918 -0.19087
Fgroupgrass:z.Soil_moisture Fgroupwoody:z.Soil_moisture
0.37120 0.19707
Fgroupgrass:z.TAIR_N Fgroupwoody:z.TAIR_N
-0.29612 -0.05893
$`348`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.VPD_N +
Fgroup:z.Soil_moisture + Fgroup:z.VPD_N + z.Soil_moisture:z.VPD_N +
1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.45795 0.08526
Fgroupwoody z.Soil_moisture
-0.02673 -0.06552
z.VPD_N Fgroupgrass:z.Soil_moisture
-0.08653 0.30382
Fgroupwoody:z.Soil_moisture Fgroupgrass:z.VPD_N
0.18475 -0.24589
Fgroupwoody:z.VPD_N z.Soil_moisture:z.VPD_N
-0.02866 0.12475
$`320`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.TAIR_N +
z.VPD_N + Fgroup:z.Soil_moisture + Fgroup:z.TAIR_N + z.Soil_moisture:z.VPD_N +
1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.45794 0.08501
Fgroupwoody z.Soil_moisture
-0.02684 -0.10473
z.TAIR_N z.VPD_N
0.16103 -0.21286
Fgroupgrass:z.Soil_moisture Fgroupwoody:z.Soil_moisture
0.37291 0.19749
Fgroupgrass:z.TAIR_N Fgroupwoody:z.TAIR_N
-0.29570 -0.05901
z.Soil_moisture:z.VPD_N
0.13200
$`448`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.TAIR_N +
z.VPD_N + Fgroup:z.Soil_moisture + Fgroup:z.TAIR_N + z.Soil_moisture:z.TAIR_N +
z.Soil_moisture:z.VPD_N + 1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.47927 0.08242
Fgroupwoody z.Soil_moisture
-0.02782 -0.09021
z.TAIR_N z.VPD_N
0.27560 -0.31517
Fgroupgrass:z.Soil_moisture Fgroupwoody:z.Soil_moisture
0.36516 0.19614
Fgroupgrass:z.TAIR_N Fgroupwoody:z.TAIR_N
-0.29793 -0.05876
z.Soil_moisture:z.TAIR_N z.Soil_moisture:z.VPD_N
-0.31673 0.47275
$`576`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.TAIR_N +
z.VPD_N + Fgroup:z.Soil_moisture + Fgroup:z.TAIR_N + z.TAIR_N:z.VPD_N +
1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.47783 0.08378
Fgroupwoody z.Soil_moisture
-0.02791 -0.07803
z.TAIR_N z.VPD_N
0.09672 -0.14884
Fgroupgrass:z.Soil_moisture Fgroupwoody:z.Soil_moisture
0.37079 0.19602
Fgroupgrass:z.TAIR_N Fgroupwoody:z.TAIR_N
-0.29567 -0.05873
z.TAIR_N:z.VPD_N
-0.10768
$`192`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.TAIR_N +
z.VPD_N + Fgroup:z.Soil_moisture + Fgroup:z.TAIR_N + z.Soil_moisture:z.TAIR_N +
1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.45319 0.08509
Fgroupwoody z.Soil_moisture
-0.02685 -0.09761
z.TAIR_N z.VPD_N
0.12938 -0.18320
Fgroupgrass:z.Soil_moisture Fgroupwoody:z.Soil_moisture
0.37325 0.19748
Fgroupgrass:z.TAIR_N Fgroupwoody:z.TAIR_N
-0.29556 -0.05901
z.Soil_moisture:z.TAIR_N
0.05334
$`96`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.TAIR_N +
z.VPD_N + Fgroup:z.Soil_moisture + Fgroup:z.VPD_N + 1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.455988 0.084770
Fgroupwoody z.Soil_moisture
-0.027072 -0.056180
z.TAIR_N z.VPD_N
0.006906 -0.088422
Fgroupgrass:z.Soil_moisture Fgroupwoody:z.Soil_moisture
0.302750 0.184306
Fgroupgrass:z.VPD_N Fgroupwoody:z.VPD_N
-0.245816 -0.028470
$`28`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.VPD_N +
Fgroup:z.Soil_moisture + 1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.45664 0.08483
Fgroupwoody z.Soil_moisture
-0.02766 -0.06058
z.VPD_N Fgroupgrass:z.Soil_moisture
-0.18548 0.32165
Fgroupwoody:z.Soil_moisture
0.18544
$`960`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.TAIR_N +
z.VPD_N + Fgroup:z.Soil_moisture + Fgroup:z.TAIR_N + z.Soil_moisture:z.TAIR_N +
z.Soil_moisture:z.VPD_N + z.TAIR_N:z.VPD_N + 1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.50762 0.08122
Fgroupwoody z.Soil_moisture
-0.02891 -0.07341
z.TAIR_N z.VPD_N
0.23841 -0.27666
Fgroupgrass:z.Soil_moisture Fgroupwoody:z.Soil_moisture
0.36323 0.19463
Fgroupgrass:z.TAIR_N Fgroupwoody:z.TAIR_N
-0.29781 -0.05847
z.Soil_moisture:z.TAIR_N z.Soil_moisture:z.VPD_N
-0.36274 0.49676
z.TAIR_N:z.VPD_N
-0.12583
$`352`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.TAIR_N +
z.VPD_N + Fgroup:z.Soil_moisture + Fgroup:z.VPD_N + z.Soil_moisture:z.VPD_N +
1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.45806 0.08540
Fgroupwoody z.Soil_moisture
-0.02677 -0.07323
z.TAIR_N z.VPD_N
0.02900 -0.11050
Fgroupgrass:z.Soil_moisture Fgroupwoody:z.Soil_moisture
0.30455 0.18470
Fgroupgrass:z.VPD_N Fgroupwoody:z.VPD_N
-0.24572 -0.02864
z.Soil_moisture:z.VPD_N
0.13274
$`480`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.TAIR_N +
z.VPD_N + Fgroup:z.Soil_moisture + Fgroup:z.VPD_N + z.Soil_moisture:z.TAIR_N +
z.Soil_moisture:z.VPD_N + 1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.47893 0.08287
Fgroupwoody z.Soil_moisture
-0.02772 -0.05888
z.TAIR_N z.VPD_N
0.14039 -0.21052
Fgroupgrass:z.Soil_moisture Fgroupwoody:z.Soil_moisture
0.29655 0.18346
Fgroupgrass:z.VPD_N Fgroupwoody:z.VPD_N
-0.24647 -0.02811
z.Soil_moisture:z.TAIR_N z.Soil_moisture:z.VPD_N
-0.30990 0.46615
$`832`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.TAIR_N +
z.VPD_N + Fgroup:z.Soil_moisture + Fgroup:z.TAIR_N + z.Soil_moisture:z.VPD_N +
z.TAIR_N:z.VPD_N + 1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.46694 0.08472
Fgroupwoody z.Soil_moisture
-0.02718 -0.09950
z.TAIR_N z.VPD_N
0.14184 -0.19383
Fgroupgrass:z.Soil_moisture Fgroupwoody:z.Soil_moisture
0.37263 0.19702
Fgroupgrass:z.TAIR_N Fgroupwoody:z.TAIR_N
-0.29554 -0.05892
z.Soil_moisture:z.VPD_N z.TAIR_N:z.VPD_N
0.12291 -0.04486
$`284`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.VPD_N +
Fgroup:z.Soil_moisture + z.Soil_moisture:z.VPD_N + 1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.45859 0.08534
Fgroupwoody z.Soil_moisture
-0.02733 -0.07161
z.VPD_N Fgroupgrass:z.Soil_moisture
-0.18932 0.32287
Fgroupwoody:z.Soil_moisture z.Soil_moisture:z.VPD_N
0.18588 0.12490
$`76`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.VPD_N +
Fgroup:z.VPD_N + 1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass Fgroupwoody
0.45595 0.08290 -0.02692
z.Soil_moisture z.VPD_N Fgroupgrass:z.VPD_N
0.12331 -0.07192 -0.26721
Fgroupwoody:z.VPD_N
-0.03978
$`332`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.VPD_N +
Fgroup:z.VPD_N + z.Soil_moisture:z.VPD_N + 1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass Fgroupwoody
0.45787 0.08340 -0.02660
z.Soil_moisture z.VPD_N Fgroupgrass:z.VPD_N
0.11309 -0.07558 -0.26732
Fgroupwoody:z.VPD_N z.Soil_moisture:z.VPD_N
-0.03998 0.12241
$`608`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.TAIR_N +
z.VPD_N + Fgroup:z.Soil_moisture + Fgroup:z.VPD_N + z.TAIR_N:z.VPD_N +
1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.47803 0.08417
Fgroupwoody z.Soil_moisture
-0.02784 -0.04644
z.TAIR_N z.VPD_N
-0.03549 -0.04657
Fgroupgrass:z.Soil_moisture Fgroupwoody:z.Soil_moisture
0.30246 0.18331
Fgroupgrass:z.VPD_N Fgroupwoody:z.VPD_N
-0.24526 -0.02805
z.TAIR_N:z.VPD_N
-0.10814
$`224`
Call:
lm(formula = Trmmol_night ~ Fgroup + z.Soil_moisture + z.TAIR_N +
z.VPD_N + Fgroup:z.Soil_moisture + Fgroup:z.VPD_N + z.Soil_moisture:z.TAIR_N +
1, data = phys_data)
Coefficients:
(Intercept) Fgroupgrass
0.453206 0.085501
Fgroupwoody z.Soil_moisture
-0.026767 -0.066327
z.TAIR_N z.VPD_N
-0.003009 -0.080515
Fgroupgrass:z.Soil_moisture Fgroupwoody:z.Soil_moisture
0.304973 0.184703
Fgroupgrass:z.VPD_N Fgroupwoody:z.VPD_N
-0.245638 -0.028639
z.Soil_moisture:z.TAIR_N
0.054983
attr(,"rank")
function (x)
do.call("rank", list(x))
<environment: 0x7fd46a6294c0>
attr(,"call")
AICc(x)
attr(,"class")
[1] "function" "rankFunction"
attr(,"beta")
[1] "none"
Finally, we’ll use the model.avg() function to create our average model and calculates relative importance. We need to specify the object that model.avg() will evaluate (in this case our top model set, top.models):
average_model<-model.avg(top.models)
To check out our final average model, use the summary() function:
summary(average_model)
Call:
model.avg(object = top.models)
Component model call:
lm(formula = Trmmol_night ~ <18 unique rhs>, data = phys_data)
Component models:
df logLik AICc delta weight
1/2/4/5/7 10 -112.22 245.25 0.00 0.14
1/2/3/4/5/6 11 -111.24 245.46 0.21 0.12
1/2/4/5/7/9 11 -111.43 245.84 0.60 0.10
1/2/3/4/5/6/9 12 -110.40 245.95 0.71 0.10
1/2/3/4/5/6/8/9 13 -109.34 246.03 0.78 0.09
1/2/3/4/5/6/10 12 -111.02 247.20 1.95 0.05
1/2/3/4/5/6/8 12 -111.05 247.26 2.02 0.05
1/2/3/4/5/7 11 -112.21 247.40 2.16 0.05
1/2/4/5 8 -115.51 247.55 2.30 0.04
1/2/3/4/5/6/8/9/10 14 -109.08 247.74 2.49 0.04
1/2/3/4/5/7/9 12 -111.37 247.89 2.65 0.04
1/2/3/4/5/7/8/9 13 -110.36 248.07 2.83 0.03
1/2/3/4/5/6/9/10 13 -110.36 248.08 2.84 0.03
1/2/4/5/9 9 -114.74 248.14 2.90 0.03
1/2/4/7 8 -115.83 248.18 2.93 0.03
1/2/4/7/9 9 -115.09 248.84 3.60 0.02
1/2/3/4/5/7/10 12 -111.99 249.14 3.90 0.02
1/2/3/4/5/7/8 12 -112.01 249.19 3.94 0.02
Term codes:
Fgroup z.Soil_moisture z.TAIR_N
1 2 3
z.VPD_N Fgroup:z.Soil_moisture Fgroup:z.TAIR_N
4 5 6
Fgroup:z.VPD_N z.Soil_moisture:z.TAIR_N z.Soil_moisture:z.VPD_N
7 8 9
z.TAIR_N:z.VPD_N
10
Model-averaged coefficients:
(full average)
Estimate Std. Error Adjusted SE z value
(Intercept) 0.46320 0.04822 0.04842 9.566
Fgroupgrass 0.08429 0.05677 0.05703 1.478
Fgroupwoody -0.02724 0.05644 0.05670 0.480
z.Soil_moisture -0.06573 0.09921 0.09955 0.660
z.VPD_N -0.16164 0.12008 0.12041 1.342
Fgroupgrass:z.Soil_moisture 0.32029 0.13875 0.13915 2.302
Fgroupwoody:z.Soil_moisture 0.18049 0.11713 0.11759 1.535
Fgroupgrass:z.VPD_N -0.11026 0.14475 0.14493 0.761
Fgroupwoody:z.VPD_N -0.01326 0.07689 0.07722 0.172
z.TAIR_N 0.08815 0.13194 0.13223 0.667
Fgroupgrass:z.TAIR_N -0.14267 0.16801 0.16818 0.848
Fgroupwoody:z.TAIR_N -0.02834 0.08439 0.08472 0.334
z.Soil_moisture:z.VPD_N 0.11882 0.20715 0.20747 0.573
z.Soil_moisture:z.TAIR_N -0.04975 0.15493 0.15518 0.321
z.TAIR_N:z.VPD_N -0.01398 0.07414 0.07440 0.188
Pr(>|z|)
(Intercept) <2e-16 ***
Fgroupgrass 0.1394
Fgroupwoody 0.6310
z.Soil_moisture 0.5091
z.VPD_N 0.1795
Fgroupgrass:z.Soil_moisture 0.0213 *
Fgroupwoody:z.Soil_moisture 0.1248
Fgroupgrass:z.VPD_N 0.4468
Fgroupwoody:z.VPD_N 0.8637
z.TAIR_N 0.5050
Fgroupgrass:z.TAIR_N 0.3963
Fgroupwoody:z.TAIR_N 0.7380
z.Soil_moisture:z.VPD_N 0.5668
z.Soil_moisture:z.TAIR_N 0.7485
z.TAIR_N:z.VPD_N 0.8509
(conditional average)
Estimate Std. Error Adjusted SE z value
(Intercept) 0.46320 0.04822 0.04842 9.566
Fgroupgrass 0.08429 0.05677 0.05703 1.478
Fgroupwoody -0.02724 0.05644 0.05670 0.480
z.Soil_moisture -0.06573 0.09921 0.09955 0.660
z.VPD_N -0.16164 0.12008 0.12041 1.342
Fgroupgrass:z.Soil_moisture 0.33849 0.11910 0.11959 2.830
Fgroupwoody:z.Soil_moisture 0.19074 0.11200 0.11250 1.696
Fgroupgrass:z.VPD_N -0.24845 0.11350 0.11400 2.179
Fgroupwoody:z.VPD_N -0.02987 0.11324 0.11375 0.263
z.TAIR_N 0.13882 0.14277 0.14319 0.969
Fgroupgrass:z.TAIR_N -0.29638 0.11438 0.11489 2.580
Fgroupwoody:z.TAIR_N -0.05886 0.11400 0.11451 0.514
z.Soil_moisture:z.VPD_N 0.24601 0.23991 0.24047 1.023
z.Soil_moisture:z.TAIR_N -0.21431 0.26104 0.26169 0.819
z.TAIR_N:z.VPD_N -0.09822 0.17417 0.17494 0.561
Pr(>|z|)
(Intercept) < 2e-16 ***
Fgroupgrass 0.13937
Fgroupwoody 0.63096
z.Soil_moisture 0.50912
z.VPD_N 0.17945
Fgroupgrass:z.Soil_moisture 0.00465 **
Fgroupwoody:z.Soil_moisture 0.08998 .
Fgroupgrass:z.VPD_N 0.02930 *
Fgroupwoody:z.VPD_N 0.79285
z.TAIR_N 0.33230
Fgroupgrass:z.TAIR_N 0.00989 **
Fgroupwoody:z.TAIR_N 0.60723
z.Soil_moisture:z.VPD_N 0.30630
z.Soil_moisture:z.TAIR_N 0.41281
z.TAIR_N:z.VPD_N 0.57449
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
This is a lot of information! We can see which component models were chosen as the top model set and then averaged, as well as their associated ranking information. We can also see the model-averaged coefficients for both the full average model and conditional average model.
The conditional average only averages over the models where the parameter appears. Conversely, the full average assumes that a variable is included in every model, but in some models the corresponding coefficient (and its respective variance) is set to zero. Unlike the conditional average, the full average does not bias the value away from zero.
We can also check out the relative importance of each factor within the model with the importance() function. Relative importance is a unitless metric ranging from 0 (doesn’t contribute to the model at all) to 1 (contributes heavily to the model). This function will also give use the number of models within the top model set that contain each factor.
importance(average_model)
Fgroup z.Soil_moisture z.VPD_N Fgroup:z.Soil_moisture
Sum of weights: 1.00 1.00 1.00 0.95
N containing models: 18 18 18 16
z.TAIR_N z.Soil_moisture:z.VPD_N Fgroup:z.TAIR_N
Sum of weights: 0.63 0.48 0.48
N containing models: 12 9 7
Fgroup:z.VPD_N z.Soil_moisture:z.TAIR_N
Sum of weights: 0.44 0.23
N containing models: 9 5
z.TAIR_N:z.VPD_N
Sum of weights: 0.14
N containing models: 4
Challenge 4
Using IT Model Averaging, create a model that tests for the effects of four factors on either transpiration or stomatal conductance. Then, create a plot that best illustrates the main finding of your top model. Ultimately, your results should be able to address one of these questions:
- What environmental variables drive nocturnal transpiration / stomatal conductance, and do these differ from the drivers of daytime transpiration / stomatal conductance?
- Are nocturnal transpiration and stomatal conductance associated with daytime physiological processes?
Key Points
Linear regression is a quick and easy way to evaluate the direct relationship between two variables.
IT Model Averaging is one approach to evaluate more complex relationships between variables.
There are often many valid approaches to address a question in R and understanding how to interpret R packages can help determine which approach might be most appropriate.